Area or mass MOI(Moment of Inertia) || Formula for moment of inertia || inertia

Area MOI || Formula for moment of inertia

The inertial moment of a lamina is a property of a 2-D shape, which characterizes its deflection under load. This is known by "Second moment of area" or the Second MOI". Moment of inertia of the zone has dimensions in length at the fourth power. Unfortunately, in engineering contexts, although it is not equivalent to the usual moment of inertia (which has dimensions in mass multiplied by the length of a square and that suffers from solids when subjected to a couple).

The second moment of the zone on the x-axis is defined as:

Area Moment of Inertia || Formula for moment of inertia and Its Application

It is represented by “I" in calculations. Interestingly, the mass moment of inertia is also represented by “I" though some difference between the mass moment of an inertia area moment of inertia exists. Area moment of inertia is that the property of a shape and is employed within the beam deflection equation:

M/I = σ/Y = E/R

From equation you'll see stress value (σ) decreases with the rise of an area moment of inertia (I) or in other words it resists beam bending or deflections. So, if you're solving a beam problem, or treating the other problem as a beam problem, then you've got to use the world moment of inertia (I). Also for calculating the utmost deflection angle and distance of various sorts of the beam, you'll be required to use area moment of inertia.

FORMING AREA IN INERTIA IS EXPLICITLY FOLLOWED || Formula for moment of inertia

Figure 1: Area MOI

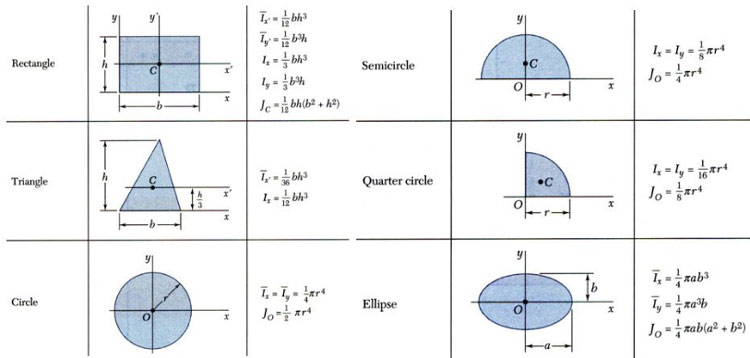
Mass MOI formulas || Formula for moment of inertia are as shown in the image below:

MAXIMUM MOMENT OF FORMULAS OF INERTIA SHOWN IN FIGURE 2 BELOW

Figure 2: Mass MOI

Want to know more about Moment of Inertia || Formula for moment of inertia and Mass Moment of Inertia (Click Here).

Kinematics of the Rigid Bodies: Click Here to study